昨日のABC155 Dでドはまりした以下の問題についてまとめてみます.
【やりたいこと】
ax <= y を満たす 整数xの範囲を求めたい。あるいは境界となる値を求めたい(Pythonで)
- a > 0の時は 条件を満たす整数xの最大値
- a < 0の時は 条件を満たす整数xの最小値
二分探索をする際に、これが正確に実装できなくて泣きをみたので、しっかり整理しておきたいと思います。
ちなみに、境界値を求める際に、ギリギリ条件を満たす値を求めるか、ギリギリ条件を満たさない値を求めるかの2通りあると思いますが、本記事はギリギリ条件を満たす値を求める方法についての記載になります。(なぜなら私がそっちの方が好きだからです)
なお、この記事で取り扱う二分探索は、答えを決め打ちして二分探索をするという問題の大枠の部分ではなく、積がある数以下となるペア数を求める際に用いる二分探索のことを指しています。(自分でも何を言っているかよくわかりません・・・)
また、言うまでもないと思いますが ax >= y になった場合はもろもろ逆になるのでご注意ください。
なぜドはまりしたのか?
ドはまり1:今回はfloat型が使えなかった
最初、二分探索の境界値を x = y / a で実装していたんですが、この方法だとfloat型になり,今回の問題だと巨大な数になるので誤差がでてしまいました。
このため,int型で取り扱うために / ではなく // で計算する必要に迫られました。(コンテスト中はここでつまづいていました・・・・)
ドはまり2:負の数がでてくる
今回の問題ではaもyも正負の制限がありません.
二分探索する境界となる整数が、y/a の切り上げなのか切り捨てなのか、はたまたそれをどの演算で入手すべきか訳がわからなくなりました。
Pythonで // 演算をする際、負の値がからむと結構ややこしくなる(少なくとも私はめちゃめちゃややこしいと思っていました)のも相まって,頭の中がカオスです。
最初に結論
- a > 0のとき: max(x) = y // a
- a < 0のとき: min(x) = -(-y//a)
上記の演算で条件を満たすxの境界値が求まります。
丁寧めに解説
以下4つのパターンに場合分けして、詳細を記載していきます。
- a > 0, y ≧ 0
- a > 0, y < 0
- a < 0, y ≧ 0
- a < 0, y < 0
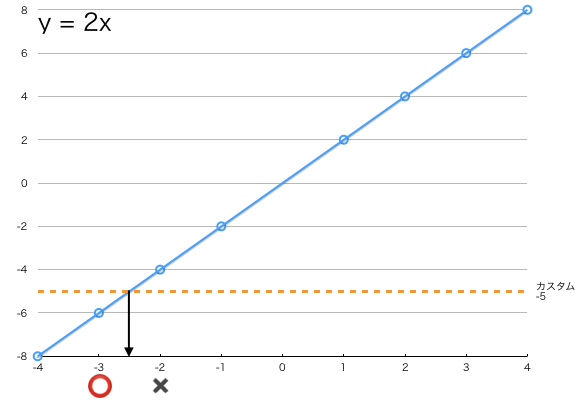
a > 0, y ≧ 0 のとき
これは簡単ですね。単純に切り捨て除算すればよいです。
# a > 0, y >= 0の時
max_x = y // a一応確認しましょう。例として y = 5, a = 2のときを考えます。
- x = 2の場合
2 * 2 = 4 で条件(ax <= 5)を満たします - x =3の場合
2 * 3 = 6 で条件(ax <= 5)を満たしません
よってギリギリ条件を満たす値:max(x) = 2となり、以下の演算で算出できています。
max_x = 5 // 2
print(max_x)
# 2a > 0, y < 0 のとき
y < 0なのでちょっと心配になりますが,上記と同じで大丈夫です
こちらも確認しましょう。y = -5, a = 2のときを考えます。
- x = -3の場合
2 * -3 = -6 で条件(ax <= -5)を満たします - x = -2の場合
2 * -2 = -4 で条件(ax <= -5))を満たしません
よってギリギリ条件を満たす値:max(x) = -3 ですがこちらも以下の演算で算出できています。
max_x = -5 // 2
print(max_x)
# -3// は切り捨て除算であるといいましたが、-2.5 を切り捨てて-3は違和感がありますよね。(負の数の四捨五入について正確な定義を知っている方ぜひ教えてください)
除算値(/で算出される値)を超えない最大の整数を返す演算と理解するといいかもしれません。あるいは数直線上の左側の整数というイメージでしょうか。(この仕様はPythonの剰余計算の思想によるものらしいです.詳しくはPython ドキュメントQ&Aを読んでください)
ここまでをまとめると、yの正負に関わらず、a > 0であれば y // a の演算で、条件をギリギリ満たすmax(x)が求まることがわかります.max(x)を超える整数xは条件(ax <= y)を満たしません。
a > 0の時はy = axが単調増加の関数になるので、除算値を超えない最大のxを返す // がぴったりはまりますね。
本題 a < 0 のとき
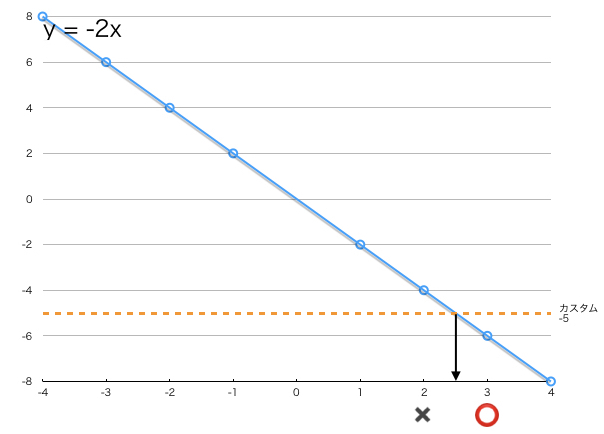
では本題に移ります。a < 0についてです。
a > 0 の時との一番の違いは y = axが単調減少の関数になるところです。
単調増加時の図と比べてわかるように、境界値は数直線で除算値の右側(切り上げ)の値になります。何を当たり前のことをと思うかもしれませんが、実際に実装しているとこんがらがってくるので、しっかり基本をおさえておいた方がバグらせずに済むと実感しています。
a < 0, y ≧ 0 のとき
欲しい境界値は x = y / a を切り上げた値なので、当然ですが a > 0のときと同じようにやると失敗します.y = 5, a = -2のときを考えます。
- x = -2の場合
-2 * -2 = 4 で条件(ax <= 5)を満たします - x = -3の場合
-2 * -3 = 6 で条件(ax <= 5)を満たしません
よってギリギリ条件を満たす値:min(x) = -2 ですが、 y // aで演算してしまうと、5//-2 = -3 となり欲しい結果が返ってきません。
5 / -2 = -2.5なので、-2.5を超えない最大の整数である-3が返ってきてしまいます。さてどうするか,次の演算も確認してから考えましょう
a < 0, y < 0 のとき
具体例として、y = -5, a = -2のときを考えます。(上のグラフで示した例です)
- x = 3の場合
-2 * 3 = -6 で条件(ax <= -5)を満たします - x = 2の場合
-2 * 2 = -4 で条件(ax <= 5))を満たしません
よってギリギリ条件を満たす値:min(x) = 3 ですが、y // a の演算では -5//-2 = 2 となり欲しい結果が返ってきません。
-5 / -2 = 2.5なので、2.5を超えない最大の整数である2が返ってきてしまいます.(個人的に一番のポイントだとおもってるのでしつこいですが繰り返しています。)
負の数がからむ切り上げの方法
もったいぶりましたが、既に述べたように、やりたいことは切り上げ(数直線上で除算値の右側の整数)を得ることです。
負の数による除算で切り上げを行うコードをいくつか紹介しますので、お好みのものを使ってください。(一応すべてのやり方でABC155 DがACすることは確認していますが,なにか間違っていたら是非コメントください)
(y + a + 1) // a
a > 0で切り上げ除算する場合に (y + a – 1) // aを使用すると思いますが,a < 0の場合は -1 ではなく +1 にすることで切り上げ除算ができます。
y // a + bool(y % a) *numpyの場合は y // a + (y % a != 0) など
切り捨て除算した後に、余りがあるなら1を足すというシンプルな発想です。(bool(y%a)は余りがあるとき1, 余りがないときは0を返します)
a > 0でも同じコードで計算できるのと、結構直感的だと思うので個人的にはお勧めです。(計算量的には、剰余計算が追加される分、上記よりやや不利です。シビアな定数倍改善が求められる場合は別の方法がいいかもしれません)
-(-y // a)
反転して切り捨ててから、もう一回反転すれば切り上げじゃないか!?という発想です。
-5 // 2 では -2.5 → -3 になってしまうところを
-(5 // 2)とすることで、2.5 → 2 → -2 のように切り上げが得られます。
まとめ
- 関数が単調増加か単調減少かちゃんと把握する
- 数直線上の左が欲しいのか、右が欲しいのか、グラフを書いて確認する
- 数直線上で左が欲しいなら切り捨て(x = y // a)
- 数直線上で右が欲しいなら切り上げ(x = -(-y // a) など)
最後の最後で申し訳ないですが、境界値を尺取りで探索していく場合は、条件式そのまま ax <= y のように演算しておけばこんな面倒なことにはならないです。
また本問題を二分探索で解こうとすると、Pythonではかなり計算時間が厳しく、numpyを使って適切にブロードキャストも駆使しながら高速化をしないとTLE します。(コンテスト中の最初の提出の時点で最適化してしまっているmaspyさんはほんとすげえです。)
numpy使いたくない人は(少ないとは思いますが)、PyPyで尺取りで判定するのが良いと思います。(ちなみにPyPy or Pythonのbisectで通せた方いたら是非コード見せてください!!!)

コメント